Как равновесие Нэша и другие понятия из теории игр применяются в криптоиндустрии, повышая ее эффективность.
Теория игр — раздел прикладной математики, изучающий модели принятия решений в ситуациях, где участники имеют несовпадающие интересы. Ее цель — определить равновесные исходы, при которых никто не может улучшить свой результат, изменив стратегию самостоятельно.
Первое математическое описание метода дал Джон фон Нейман в статье «К теории стратегических игр» (1928). К этой работе восходит понятие «игры с нулевой суммой», в которой победа одного участника всегда подразумевает поражение другого. В ней исключена возможность взаимной выгоды или потери: победитель забирает все.
И, напротив, играми с ненулевой суммой называют такие, которые допускают общие победы или поражения. Они более адекватно отражают в том числе экономические процессы, но при этом гораздо сложнее высчитываются.
Простой пример — бизнес-партнерство. Два предпринимателя решают вопрос о сотрудничестве. Если каждый действует в одиночку, они зарабатывают по $10 000. Объединив усилия, они получат доход $30 000 — по $15 000 каждому. В случае обмана (например, присвоения прибыли) недобросовестный партнер может получить $28 000, тогда когда второй — лишь $2000.
Таким образом, сумма выигрышей непостоянна и напрямую зависит от поведения участников. Но все могут получить больше сотрудничая, а не действуя в одиночку.
В 1950 году аспирант Принстонского университета Джон Форбс Нэш опубликовал короткую статью. В ней он доказал: любая игра с ограниченным числом участников и стратегий имеет хотя бы одну точку равновесия, где никто не может улучшить свой результат, действуя в одиночку.
Равновесие Нэша — это состояние, когда все игроки выбрали такие стратегии, что никому не выгодно менять свой выбор, если другие остаются при своем. Например, два или более предпринимателей решают, снижать ли цены. Если один демпингует, другие вынуждены скопировать поведение, чтобы не потерять клиентов. В итоге все участники рынка оказываются в равновесии, где любое одностороннее изменение приведет к потере прибыли.
Честная игра — рациональная стратегия, формирующая равновесие Нэша. В блокчейне это может проявляться в поведении майнеров: атаковать сеть невыгодно, потому что падение доверия обесценивает награду.
Позже ученый развил идею в работах «Некооперативные игры» (1951) и «Кооперативные игры на две персоны» (1953).
Джон Форбс Нэш, 1951 год. Источник: Wikimedia.
Идея нобелевского лауреата стала математическим описанием устойчивого баланса интересов и краеугольным камнем современной теории принятия решений.
В 1967–1968 годах Джон Чарльз Харсаньи в серии статей представил равновесие в условиях неполной информации. Для этого он использовал сформулированную двумя столетия ранее формулу Томаса Байеса.
Байесовское равновесие используется в условиях неполной информации — когда игроки не знают точно о стратегиях друг друга. Практическое применение оно нашло, например, в DeFi-протоколах. Так, в 2023 году коллектив сотрудников Колумбийского университета (Нью-Йорк) опубликовал работу «Майерсоновская модель оптимального предоставления ликвидности в автоматизированных маркетмейкерах».
В ней авторы изложили теоретическую модель, объясняющую, как участники с разной осведомленностью о рынке могут рационально предоставлять ликвидность в DeFi-пулы для достижения равновесия между риском, комиссией и вознаграждением.
Она построена с использованием байесовского анализа — каждый поставщик ликвидности выбирает стратегию, исходя из своих вероятностных ожиданий относительно поведения других участников и состояния рынка.
В 1973 году Джон Мейнард Смит и Джордж Прайс описали стратегию, которая не может быть вытеснена альтернативной, если принята большинством. Их работа «Логика конфликтов у животных» перенесла теорию игр в биологию и поведенческие науки.
Классическая игра Смита «Ястребы и голуби» доказала, что агрессоры выигрывают лишь до определенного предела. Когда популяция хищников значительно вырастает, конфликты делают стратегию убыточной.
В популяции есть два типа игроков: ястребы (агрессивные) и голуби (мирные). Они конкурируют за ограниченный ресурс (например, еду или территорию).
Игроки представляют две стратегии:
Результаты игры:
Поэтому возникает равновесие — стабильная доля ястребов и голубей, при которой никто не может улучшить свое положение. Это и есть эволюционно стабильная стратегия (ЭСС).
ЭСС можно применять как в традиционной, так и в криптоэкономике. Она демонстрирует баланс между агрессивными (спекулянтами) и кооперативными (долгосрочными участниками) игроками.
В исследовании 2021 года Шашанк Мотепалли и Ханс-Арно Якобсен из Университета Торонто постарались глубже понять особенности таких произвольных систем вознаграждения.
Они разработали единую теоретическую модель для PoS-блокчейнов. Авторы формализовали игру валидации блоков, в рамках которой вознаграждения распределяются между участниками за корректное подтверждение.
Источник: arXiv.
С помощью ЭСС они исследовали, как со временем может изменяться поведение участников в зависимости от выбранного механизма вознаграждений. Ученые пришли к выводу, что штрафы играют ключевую роль в поддержании целостности и безопасности блокчейна.
В 1974 году научное сообщество узнало о коррелированном равновесии Роберта Ауманна. Оно предполагает координацию действий игроков через некий единый центр информации, предоставляющий рекомендации.
На их основе каждый игрок выбирает собственную стратегию. Никто не может увеличить свое вознаграждение, отклонившись от полученного совета, если все игроки следуют рекомендациям. Концепция важна для децентрализованных систем и ДАО, где решения принимаются синхронно.
Со временем подобные модели становились все более приближенными к реальности. В 1980-х изучение динамического и стохастического равновесия позволило применять теорию в современной экономике, алгоритмах машинного обучения, архитектуре алгоритмов консенсуса блокчейнов и токеномике.
Поведенческая теория игр, ставшая популярной в 1990-х, учитывает психологические и социальные факторы. Ограниченная рациональность, эмоции и личные предпочтения позволяют достаточно точно спрогнозировать поведение акторов.
Наглядной и доступной иллюстрацией к моделям теории игр служит интерактивный проект «Эволюция доверия», основанный на трудах Роберта Аксельрода и Роберта Патнэма.
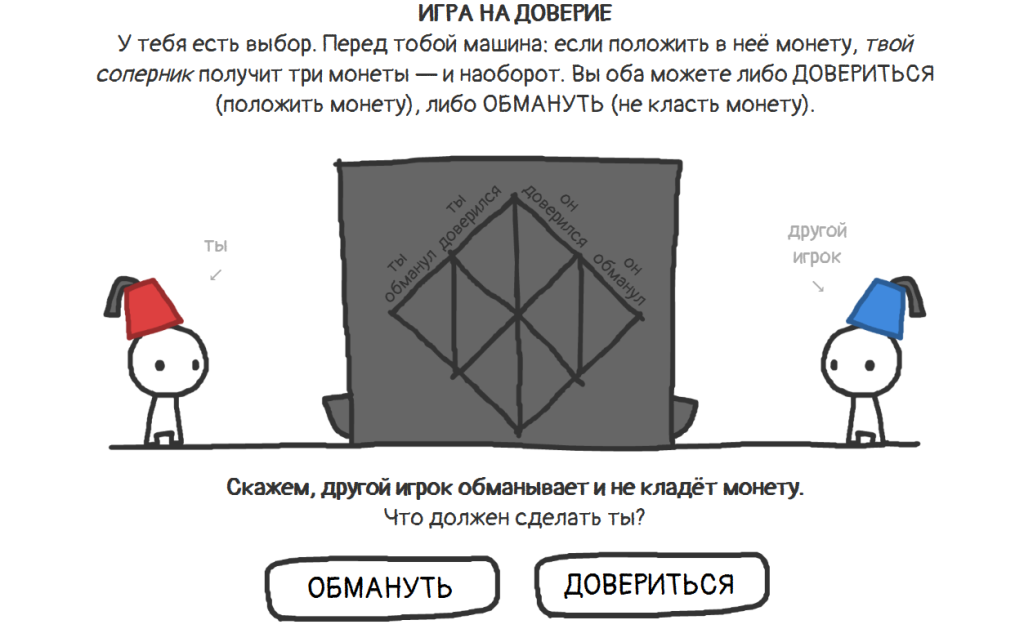Веб-игра «Эволюция доверия». Скриншот: ForkLog.
В классической игре «Дилемма заключенного» полиция по отдельности допрашивает двух подозреваемых. Им нужно прийти к консенсусу: признаться или молчать.
Если оба откажутся свидетельствовать, они получат легкое наказание. В случае признания одного и молчания другого — первый выйдет на свободу, а второй получит суровый приговор. Если оба пойдут на сотрудничество со следствием, их наказание будет умеренным.
Поскольку ни один из заключенных не может улучшить свое положение, изменив выбор в одностороннем порядке, стратегия признания становится равновесием по Нэшу.
В контексте майнинга криптовалют эта игра помогает объяснить, почему добытчики, например, биткоина часто действуют в личных интересах, даже если это вредит системе в целом.
Допустим, в пуле участвуют два майнера. Они могут выбрать из следующих стратегий:
Чтобы уменьшить такие риски, сети внедряют механизмы штрафов и вознаграждений.
В криптоиндустрии теория игр помогает создать структуру вознаграждений, при которой честное экономическое поведение не только безопаснее, но и выгоднее.
Мошенничество становится настолько неэффективным и затратным, что для рациональных участников, движимых прибылью, оно выходит за пределы разумных стратегий.
Механизмы, которые усилили доверие:
В статье «Взгляд на теорию игр биткоина», опубликованной в Bitcoin Magazine, воспроизведена шахматная партия между цифровым и государственными институтами.
Доминирующая стратегия первой криптовалюты в этой игре — продолжать существовать вопреки атакам со стороны правительств или финансовых организаций.
Авторы использовали реальные исторические ситуации, угрожавшие биткоину: запрет майнинга в Китае, введение криптоналогов в США, экологические инициативы против добычи цифрового золота, конфликт между МВФ и Сальвадором.
Эти события связали с базовыми понятиями теории игр, построив матрицу выигрышей и определив равновесие Нэша.
Здесь участники сети биткоина имеют следующие варианты:
Институты также располагают двумя возможными стратегиями:
Матрица выигрышей:
Равновесие Нэша достигается, когда институты атакуют, а биткоин продолжает существовать. Игра отразила реальную ситуацию того времени: несмотря на постоянное давление, первая криптовалюта оставалась устойчивой и жизнеспособной.
Сейчас равновесие нарушено: криптовалюты попали в зону интересов государств и традиционных финансов.
JOIN
